Computation of the n'th digit of pi in any base in O(n^2)
Fabrice Bellard
This article is an alpha version. Please send any comments to Fabrice.Bellard@enst.fr
Simon Plouffe explained in [1] a new algorithm to compute the
n'th digit of  and some other mathematical constants in any base with
very little memory. Its running time is
and some other mathematical constants in any base with
very little memory. Its running time is 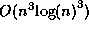 . We
present here an improvement of this algorithm whose running time is
. We
present here an improvement of this algorithm whose running time is
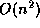 while its memory requirements stay
while its memory requirements stay 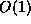 , which makes it
practical to compute the millionth digit of
, which makes it
practical to compute the millionth digit of  for example.
for example.
We want to compute the n'th digit in base B of s, where
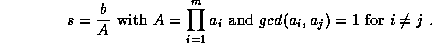
Let 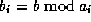 ,
, 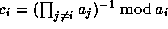 and
and
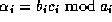 . We have
. We have
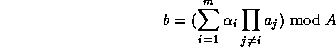
with the Chinese remainder theorem. Hence
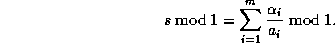
The 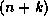 'th digits of s, where
'th digits of s, where 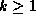 , are the digits in base B of
, are the digits in base B of

With the last formula we have
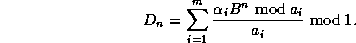
As shown in [1], this equality is interesting because each term
can be computed separatly, with a total memory of 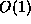 if we already
know b and
if we already
know b and 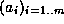 .
.
We want now to compute the n'th digit in base B of 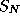 , where
, where

with
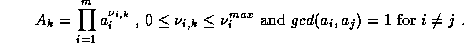
With the first result we have

where
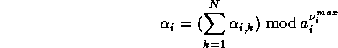
with

and

The key observation is that we can use for all 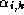 the same
modulo, hence
the same
modulo, hence
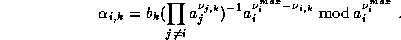
This can be rewritten
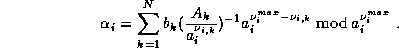
To have the digits after the n'th one, in base B, we compute
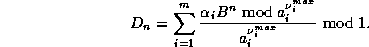
The running time is 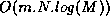 and the memory requirements stay
and the memory requirements stay
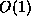 if we suppose that:
if we suppose that:
Given
we can use the result of section 2 because if p is a
prime number, we notice that
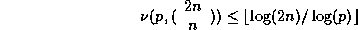
where 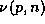 is the multiplicity of
p in n. It comes from the relation
is the multiplicity of
p in n. It comes from the relation
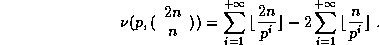
Hence, if we want the n'th digit of  in base B, we may use the
following algorithm:
in base B, we may use the
following algorithm:
-
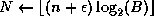 where
where
 is a small integer to ensure we have the precision needed
;
is a small integer to ensure we have the precision needed
; 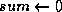 .
.
- For each prime number a with 2 < a < 2N, do:
- If we suppose that
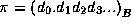 , then, if we
neglect rounding errors,
, then, if we
neglect rounding errors,
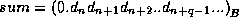 . The number q of
correct digits depends on
. The number q of
correct digits depends on  .
.
The running time is 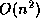 because there are
because there are 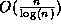 prime numbers between 2 and 2n . The memory requirements are, as
expected, in
prime numbers between 2 and 2n . The memory requirements are, as
expected, in 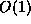 .
.
We have presented an algorithm to compute the n'th digit in any base B of
 whose running time is
whose running time is 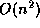 . It has the same running time as other
classical methods for computing
. It has the same running time as other
classical methods for computing  (e.g. arctangent formulas), but it
uses little memory, it is very simple and does not need high precision
computations. It is still slower than the BBP algorithm [2], but it
works in any base. As described in [1], the same algorithm may
be used to compute other numbers such as
(e.g. arctangent formulas), but it
uses little memory, it is very simple and does not need high precision
computations. It is still slower than the BBP algorithm [2], but it
works in any base. As described in [1], the same algorithm may
be used to compute other numbers such as 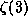 ,
, 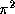 ,
, 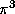 ,
,
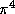 and
and 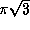 .
.
References
- 1
- Simon Plouffe, On the computation of the n'th
decimal digit of various transcendental numbers, November 1996.
- 2
- David H. Bailey, Peter B. Borwein and
Simon Plouffe, On the Rapid Computation of Various Polylogarithmic
Constants, April 1997 in Mathematics of Computation.
Sun Jan 12 22:34:36 MET 1997
Fabrice Bellard (
https://bellard.org/ )
 and some other mathematical constants in any base with
very little memory. Its running time is
and some other mathematical constants in any base with
very little memory. Its running time is 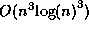 . We
present here an improvement of this algorithm whose running time is
. We
present here an improvement of this algorithm whose running time is
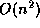 while its memory requirements stay
while its memory requirements stay 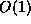 , which makes it
practical to compute the millionth digit of
, which makes it
practical to compute the millionth digit of  for example.
for example.
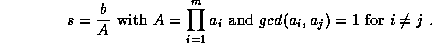
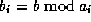 ,
, 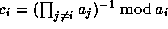 and
and
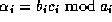 . We have
. We have
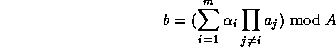
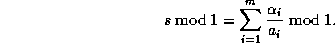
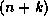 'th digits of s, where
'th digits of s, where 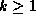 , are the digits in base B of
, are the digits in base B of

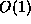 if we already
know b and
if we already
know b and 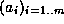 .
.
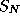 , where
, where

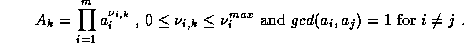

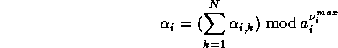


 the same
modulo, hence
the same
modulo, hence
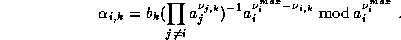
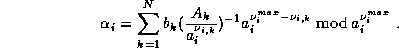
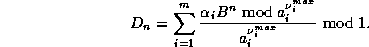
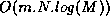 and the memory requirements stay
and the memory requirements stay
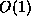 if we suppose that:
if we suppose that:
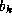 ,
, 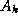 ,
, 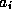 ,
, 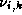 and
and 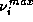 are given.
are given.
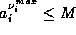 for every i. We suppose that M fits in
a computer word so that each operation takes a time of
for every i. We suppose that M fits in
a computer word so that each operation takes a time of 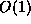 except the
modulo inversion which takes a time of
except the
modulo inversion which takes a time of 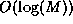 .
.
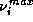 is small so an exponentiation by it takes a time of
is small so an exponentiation by it takes a time of 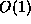 .
.
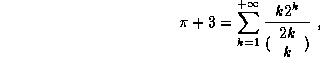
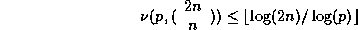
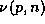 is the multiplicity of
p in n. It comes from the relation
is the multiplicity of
p in n. It comes from the relation
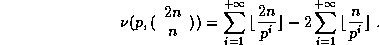
 in base B, we may use the
following algorithm:
in base B, we may use the
following algorithm:
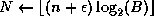 where
where
 is a small integer to ensure we have the precision needed
;
is a small integer to ensure we have the precision needed
;  .
.
 ;
;
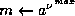 .
.
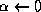 ;
;
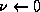 ;
;
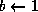 ;
;
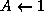 .
.
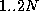 do:
do:
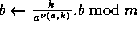 ;
;
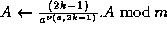 ;
;
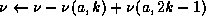 .
.
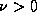 do:
do: 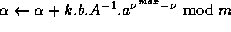 .
.
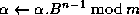 ;
;
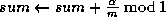 .
.
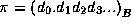 , then, if we
neglect rounding errors,
, then, if we
neglect rounding errors,
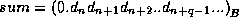 . The number q of
correct digits depends on
. The number q of
correct digits depends on  .
.
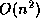 because there are
because there are 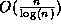 prime numbers between 2 and 2n . The memory requirements are, as
expected, in
prime numbers between 2 and 2n . The memory requirements are, as
expected, in 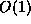 .
.
 whose running time is
whose running time is 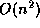 . It has the same running time as other
classical methods for computing
. It has the same running time as other
classical methods for computing  (e.g. arctangent formulas), but it
uses little memory, it is very simple and does not need high precision
computations. It is still slower than the BBP algorithm [
(e.g. arctangent formulas), but it
uses little memory, it is very simple and does not need high precision
computations. It is still slower than the BBP algorithm [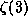 ,
, 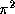 ,
, 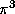 ,
,
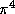 and
and 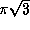 .
.