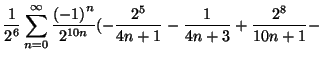 |
|||
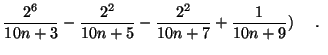 |
(1) |
Fabrice Bellard
January 20, 1997
We describe here a mean to find formulas similar to those in [1]. We
show in particular that
This formula is very interesting because, with the algorithm described in
[1], it enables us to compute the ![]() th binary digit of
th binary digit of ![]() 43%
faster than the previous known formula [1]:
43%
faster than the previous known formula [1]:
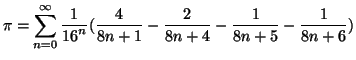 |
(2) |
The method to get formulas such as (1) is in fact very simple.
We use that
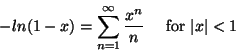
In particular
With
![]() in (3) we get
in (3) we get
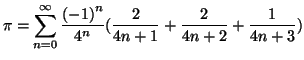 |
(5) |
Some classical arctangent relations give interesting results:
In particular, we obtain from (6) and (3)
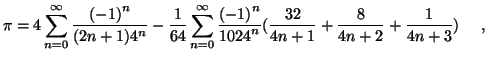 |
The existence of a formula faster than (1) to calculate
the ![]() th binary digit of
th binary digit of ![]() remains an open question.
remains an open question.